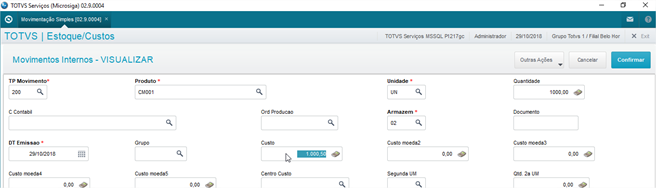
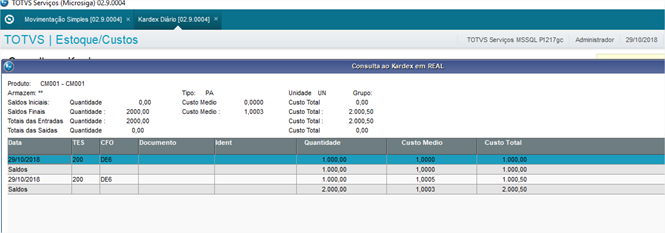
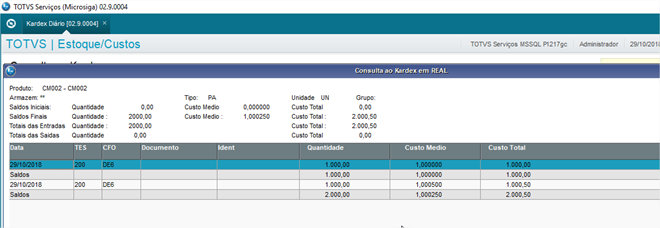
Esta documentação visa exemplificar um cenário simples de movimentação e o resultado obtido no calculo do custo médio.

O calculo do custo médio pode ter diferentes resultados dependendo da configuração do numero de decimais usada no sistema. 

Um exemplo pratico para figurar isto é quando temos processos de movimentações que usam a movimentação valorizada de estoque.

Supondo que o cliente use o custo unificado por filial (MV_CUSFIL = F) numa empresa que tenha dois armazéns. Em cada um deles destes armazéns são efetuados movimentos valorizados de estoque com custos diferentes para o mesmo produto, e conforme a precisão padrão do sistema, o custo médio da junção dos armazéns será de acordo com esta precisão. Exemplo :

- Produto CM001

- Saldo inicial no armazém 01 igual á zero.

- Saldo inicial no armazém 02 igual á zero.

- Movimento de devolução valorizado no armazém 01 com quantidade 1000 e valor 1000,00.

- Movimento de devolução valorizado no armazém 02 com quantidade 1000 e valor 1000,50.

Se consultar o Kardex Diario Diário do produto veremos que o custo médio deste produto dos dois armazéns encontra-se calculado de acordo com a configuração e precisão de 4 casas decimais no custo médio.

Isto se dá da seguinte forma :

Armazém 01 , qtde 1000 valor 1000,00 portanto custo médio será 1000,00 / 1000 = 1,0000

Armazém 02 , qtde 1000 valor 1000,50 portanto custo médio será 1000,50 / 1000 = 1,0005

O custo médio dos dois armazéns será a soma das qtdes e valores usando o mesmo critério :

Qtde 1000 + 1000 = 2000

valor 1000,00 + 1000,50 = 2000,50

então 2000,50 / 2000 = 1,00025

Como o sistema esta usando a precisão de 4 decimais no custo médio, o resultado acima será ajustado usando o critério de arredondamento universal com 4 decimais  decimais, sendo  : Então 1

 1,00025 em 4 decimais será 1,0002, porem como a próxima casa do numero depois das decimais usadas é maior ou igual a 5 ocorre o arredondamento universal, e este valor será 1,0003.

Se usarmos este custo médio para reverter ao valor de entrada, Então :

Custo medio 1,0003 * qtde 2000 = 2000,60

Se subtrairmos a soma das entradas deste valor revertido, então ;

2000,60 - 2000,50 = 0,10 de diferença.

Observe que não falamos de recalculo do custo médio, pois o efeito já ocorre nativamente no Sistema devido a precisão das decimais, e executar o recalculo, não irá corrigir o problema nativo de precisão.

Caso seja aumentada a precisão de decimais, ajustado os campos B2_CM1, B2_CMFIM1 e B9_CM1 para 6 decimais (claro que somente estes campos apenas para figurar este cenário) refazendo o mesmo cenário agora para o produto CM002, observe que não ocorre o truncamento/arredondamento de valor e o custo médio dos armazéns fica mais preciso.-

Custo médio 1,00025 * qtde 2000 = 2000,50 – soma das movimentações 2000,50 = 0 de diferença.

Muitos clientes conhecem e sabem deste efeito, e que sempre poderá ocorrer isto quando o resultado do calculo cair na situação de dízima periódica, por exemplo :

3000,00 + 3000,40 = 6000,40

6000,40 / 3000 = 2,0001333333333333333333333333333

Alguns destes clientes optam em criar movimentos apenas de valores de contrapartida para zerar o saldo da diferença de valor, outros preferem resolver esta diferença na parte contábil, mas para os casos em que esta diferença for menor ou igual a 0,01 o Sistema zera automaticamente.